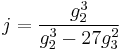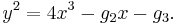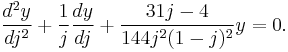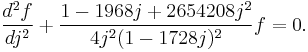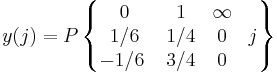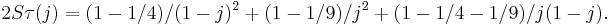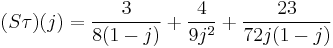Picard–Fuchs equation

In mathematics, the Picard–Fuchs equation, named after Charles Émile Picard and Lazarus Fuchs, is a linear ordinary differential equation whose solutions describe the periods of elliptic curves.

1 Definition
2 Solutions
3 Identities
4 Generalization
5 References

Definition

Let

$j=\frac{g_2^3}{g_2^3-27g_3^2}$

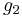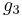be the j-invariant with $g_2$ and $g_3$ the modular invariants of the elliptic curve in Weierstrass form:

$y^2=4x^3-g_2x-g_3.\,$

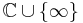Note that the j-invariant is an isomorphism from the Riemann surface H/ $\Gamma$ to the Riemann sphere $\mathbb{C}\cup\{\infty\}$ ; where H is the upper half-plane and Γ is the modular group. The Picard–Fuchs equation is then

$\frac{d^2y}{dj^2} %2B \frac{1}{j} \frac{dy}{dj} %2B \frac{31j -4}{144j^2(1-j)^2} y=0.\,$

Written in Q-form, one has

$\frac{d^2f}{dj^2} %2B \frac{1-1968j %2B 2654208j^2}{4j^2 (1-1728j)^2} f=0.\,$

Solutions

This equation can be cast into the form of the hypergeometric differential equation. It has two linearly independent solutions, called the periods of elliptic functions. The ratio of the two periods is equal to the period ratio τ, the standard coordinate on the upper-half plane. However, the ratio of two solutions of the hypergeometric equation is also known as a Schwarz triangle map.

The Picard–Fuchs equation can be cast into the form of Riemann's differential equation, and thus solutions can be directly read off in terms of Riemann P-functions. One has

$y(j)=P \left\{ \begin{matrix} 0 & 1 & \infty & \; \\ {1/6} & {1/4} & 0 & j \\ {-1/6\;} & {3/4} & 0 & \; \end{matrix} \right\}\,$

For an explicit formula of an inverse of the j-invariant see the article listed first in the references.

Dedekind defines the j-fn by its Schwarz derivative in his letter to Borchardt. As a partial fraction, it reveals the geometry of the fundamental domain: Here the first term is in error. We should see:

$2S\tau(j) = (1-1/4)/(1-j)^2 %2B (1-1/9)/j^2 %2B (1-1/4-1/9)/j(1-j). \,$

Identities

This solution satisfies the differential equation

$(S\tau)(j)=\frac{3}{8(1-j)}%2B\frac{4}{9j^2}%2B\frac{23}{72j(1-j)}$

where (Sƒ)(x) is the Schwarzian derivative of ƒ with respect to x.

Generalization

In algebraic geometry this equation has been shown to be a very special case of a general phenomenon, the Gauss–Manin connection.

References

Adlaj, Semjon (2011). "An inverse of the modular invariant". arXiv:1110.3274 [math.NT].

J. Harnad and J. McKay, Modular solutions to equations of generalized Halphen type, Proc. R. Soc. London A 456 (2000), 261–294,

(Provides a readable introduction, some history, references, and various interesting identities and relations between solutions)

J. Harnad, Picard–Fuchs Equations, Hauptmoduls and Integrable Systems, Chapter 8 (Pgs. 137–152) of Integrability: The Seiberg–Witten and Witham Equation (Eds. H.W. Braden and I.M. Krichever, Gordon and Breach, Amsterdam (2000)).

(Provides further examples of Picard–Fuchs equations satisfied by modular functions of genus 0, including non-triangular ones, and introduces Inhomogeneous Picard–Fuchs equations as special solutions to isomonodromic deformation equations of Painlevé type.)